Home Work 2/27/2016

Here is the next week's  Home Work and Geometric Sense

LCM AND GCF

Factor

When a whole number is divided into another whole number without a remainder, it is called a factor.

Factors are either composite numbers or prime numbers (except that 0 and 1 are neither prime nor composite).

Example: The number 6 is a factor 54, because it goes into 54 evenly 9 times. In this case 9 is also a factor of 54.

Example:2 and 3 are factors of 6,because 2 × 3 = 6.

Example:3 is a factors of 9, because 3 × 3 = 9. 

Note: Prime numbers only have 2 factors: 1 and itself

Prime Factors

All factors of a number that are prime are called prime factors.

Prime Factorization

The Prime Factorization of a number is written as the product of all its prime factors.

Common Factor

A common factor is a whole number that is a factor of two or more nonzero whole numbers.

Example: 3 is a common factor of the numbers 15 and 24. Both 15 and 24 have 3 as a factor, therefore 3 is called “common” between 15 and 24.

  

Greatest Common Factor

The greatest common factor, or GCF, is the greatest factor that divides two numbers.

Different methods to find GCF

There are 3 methods for finding the GCF.

1   Method 1. Rainbow method 

Example: Find the GCF of 14, 35.

List all the factors

14: 1, 2, 7, 14

35: 1, 5, 7, 35

Common factors: 1, 7

GCF: 7

     Method 2.  Factor Tree method 

                Example: Find the GCF of 18, 24

                step 1: List all the factors using factor tree

                           18 = 2x3x3,  24 = 2x2x2x3

                step 2: Identify the common factors

                           The common factors of 18 and 24 are 2 and 3. 

                Step 3: Multiply the common factors to find the GCF.

                           GCF = 3x2 = 6

            Method 3. CAKE or ladder Method

      

Step 1:

Divide the numbers by the prime number until the numbers cannot be divided evenly

Step 2:

     Multiply all prime numbers used to divide. 

Multiple

The multiple, x, of a number, n, is a number where n is a factor of x.

Example: The number 33 (x) can be divided by 3 (n) without any remainder. So 33 is a multiple of 3 (3 * 11 = 33).

Common multiple

A common multiple is a number that is a multiple of two or more numbers. The common multiples of 3 and 4 are 12, 24, 36...

Least common multiple (LCM)

The least common multiple (LCM) is the smallest number that is a multiple of two or more numbers.

Example: The LCM of 2, 3, 4, and 6 is 12.

Different methods to find LCM

Method 1: Listing  Multiples

Find LCM of 3 and 4

Step 1:

List all multiples of 3 and 4

Step 2: 

find common multiples

Step 3:

Find least common multiple

Method 2: Using Prime Factorization

Step 1: 

Identify Common factors 

common factors for 18 and 24 are 3 and 2

step 2:

Multiply common factors with all other factors

Other factors for 18 is 3 , other factors for 24 are 2 and  2

Step 3:

Multiply the common factors with other factors

LCM = 2x3x3x2x2= 72

Method 3: ladder method

Relationship between the GCF and LCM

The product of the GCF and the LCM of two or more numbers is equal to the product of the numbers:

      GCF (a, b) · LCM (a, b) = a · b

      LCM (a,b) is read as "LCM of numbers a and b"

      GCF (a,b) is read as "GCF of numbers a and b"

Example:

    GCF (12, 16) = 4

   LCM (12, 16) = 48

   48 · 4 = 12 ·16

   192 = 192

Homework due 2/21/16

Here is next week's homework. It is Expressions and Equations  and  Worksheet 1.

Meeting of 2/14/16

 We did the Long Problem and discussed about classification of numbers.

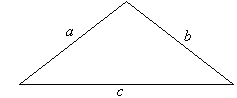
Pythagorean Theorem

The Pythagorean Theorem states that when the squares of sides a and b on a right triangle are added up, it equals the square of side c, the hypotenuse of the triangle. 

It is more commonly known as

a² + b² = c².

(a and b are legs or sides and c is the hypotenuse)

When each of the sides of a right triangle has a whole number length, the three numbers are called a Pythagorean triple.  

Some of the Pythagorean triples are listed below:

(3,4,5) (5,12,13) (7,24,25) (8,15,17) (9,40,41) (11,60,61) (12,35,37) (13,84,85) (16,63,65) (20,21,29) (28,45,53) (33,56,65) (36,77,85) (39,80,89) (48,55,73) (65,72,97)

Triangles and Angles

Types of Triangle

• Equilateral triangle: Has 3 sides of equal length and three equal angles (Always 60 degrees).
• Equiangular Triangle: All three angles are equal.
• Isosceles triangle: Has 2 sides of equal length and two equal angles.
• Scalene triangle: Has no sides of equal length and no equal angles.
• Acute triangle: All angles are less than 90 degrees
• Right triangle: One angle are 90 degrees.
• Obtuse triangle: One angle is more than 90 degrees.

Types of Angles

• Acute Angle: An angle less than 90 degrees
• Obtuse Angle: An angle more than 90 degrees but less than 180 degrees
• Right Angle: An angle equaling 90 degrees
• Straight Angle: An angle equaling 180 degrees
• Reflex Angle: An angle more than 180 degrees but less than 360 degrees
• Interior Angle: The three angles on the inside of a triangleExterior Angle: The angle between a side of a triangle and the extension of an adjacent side.

A triangle can be more than one type at the same time.

For example:

• A scalene triangle can have one interior angle 90 degrees, (making it also a right triangle) and is called a "right scalene triangle"
• An isosceles triangle has a right angle is called a "right isosceles triangle"

Formula for Perimeter of a Triangle:

The perimeter is the distance around the edge of the triangle.

Perimeter = A+B+C

Formula for Area of a triangle

The area is half of the base times height.

Area =1/2bh or A=bh/2

Facts 1.     A triangle has three sides and three angles. 2.     The three angles always add to 180 degree. 3.     The sum of the lengths of any two sides of a triangle is always longer than the third side. 4.     The longest side of a right angle triangle is called the hypotenuse, it is always found opposite the right angle. 5.     The shortest side is always opposite the smallest interior angle 6.     The longest side is always opposite the largest interior angle. 7.     The interior angles of a triangle always add up to 180° 8.     The exterior angles of a triangle always add up to 360°

Meeting of 2/7/16

Last week we did the Long Problem worksheet as well as the Measurement worksheet.

Classification of Numbers

Every number can be classified into one or more groups. So numbers can be classified as rational or irrational, natural, whole, or integer.

Natural Numbers

Natural Numbers are Counting Numbers.

For Example: 1, 2, 3, 4, 5 ……….

Even Numbers

Multiples of 2 are even numbers. Even Numbers are also Natural numbers

For Example: 2, 4, 6, 8, 10……………

Odd Numbers

Numbers which are not multiples of 2 are odd numbers. Odd numbers are also natural numbers

For Example: 1, 3, 5, 7 …

Prime Number

A prime number is a positive integer that has exactly two positive integer factors, 1 and itself. 

First few prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37…

Co-prime

No common factors other than 1.
Example: 21 and 22 are coprime (the only common factor is 1)
• The factors of 21 are 1, 3, 7 and 21
• The factors of 22 are 1, 2, 11 and 22
Co-prime also called "relatively prime" or "mutually prime".

Twin Primes

Twin Primes are Successive odd numbers that are both Prime numbers.

For Example: (3, 5), (5, 7), (11, 13)...

Composite Number

Composite Numbers are values that can be factored into two or more values other than one (1) and itself.

First few composite numbers: 4,6,8,9,10,12,14,15,16,18,20,21………..

Whole Numbers

Whole Numbers include ALL natural numbers plus 0.

For Example: 0, 1, 2, 3…

Integers

Integers include ALL whole numbers as well as negative numbers

For Example: -3,-2,-1, 0, 1, 2, 3 …

Negative Integers:  … -5, -4, -3, -2, -1

Positive Integers: 1, 2, 3, 4, 5...

Non-Negative Integers: 0, 1, 2, 3, 4, 5...

Perfect numbers

Perfect number is a positive integer that is equal to the sum of its proper divisors.

Example 1: 6 (proper factors: 1, 2, 3) is a Perfect number because 1+2+3=6.

Example 2: 28 (proper factors: 1, 2, 4, 7, 14) is also a Perfect number, because 1+2+4+7+14=28.

Rational Numbers

Rational Numbers are any number that can be written as a fraction.

For Example: 3/5,-4/9     

Rational numbers can also be represented as decimals.

Example: 4/5 = 0.8, -27/4 =-6.75, 2/3= 0.66666 (6 is repeating)

Fractions

A fraction tells us how many parts of a whole we have.

For Example: 1/3 means 1 out of 3

Proper fraction

A fraction that is less than 1. The numerator is smaller than the denominator.

For Example: 2/3

Improper fraction

A fraction greater than or equal to 1.

For Example: 1/5, 2/5, 4/4

Mixed fraction

A whole number plus a proper fraction.

For Example: 2 1/3= 2+1/3

Irrational Numbers

An irrational number is a decimal that neither terminates (stops like 0.25) nor repeats (0.333333).

For Example: π= 3.14159265359…, sqrt (2) = 1.414213562… (these decimals continue)

If a number is rational, then it cannot be irrational

Real Numbers

Real Numbers includes both the rational and irrational numbers

For Example: 3, 5.68, -0.435, 5/6, sqrt (3), 176

Imaginary Numbers

A number that when squared gives a negative result. Represented by i.

i=sqrt (-1)
If you square any Real Number you always get a positive, or zero, result.

Example both 2×2, and (-2) × (-2) are equal to 4.

How can we square a number to get a negative result?

We "imagine" that we can …, which may seem impossible, is actually useful and can solve real problems.

Complex Numbers

A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit, that satisfies the equation i² = −1.

For Example: 3 + 2i, 27.2 - 11.05i

Homework due 2/14/16

Here is next week's homework. It is on Geometry and Statistics and Probability.

Homework Due 2/7/16

Hello!

Here is a page on Number Sense and Measurement. We will correct it at this coming meeting.

Registration Info

Just a reminder that registration for math olympiad is open.
Here is the link!
We will discuss more about it during this week's meeting on Sunday.

Welcome Olymath!

Welcome students and parents!

I'm grateful to be teaching math to our young group of kids for Math Olympiad!

Let's be sure to have lots of fun as we solve math problems!

Click here to get to the Math Olympiad Home Page!